Как решать проценты, Задачи на нахождение процента

Цель работы. Готовимся к школе. Илья Московец Профиль Благодарили: 0 Сообщений: 1. Обратите внимание: волшебный крестик показывает, что числа, соединенные отрезком, следует перемножить и полученные произведения приравнять.
К примеру, нужно узнать содержание какого-либо вещества в продукте или найти цену товара со скидкой. Научимся решать задачи на проценты легко и быстро!
Эмили проходит курс по математике, который содержит 25 разделов. Она знает, что она завершила уже 7 разделов. Какой процент от всего курса освоила Эмили?
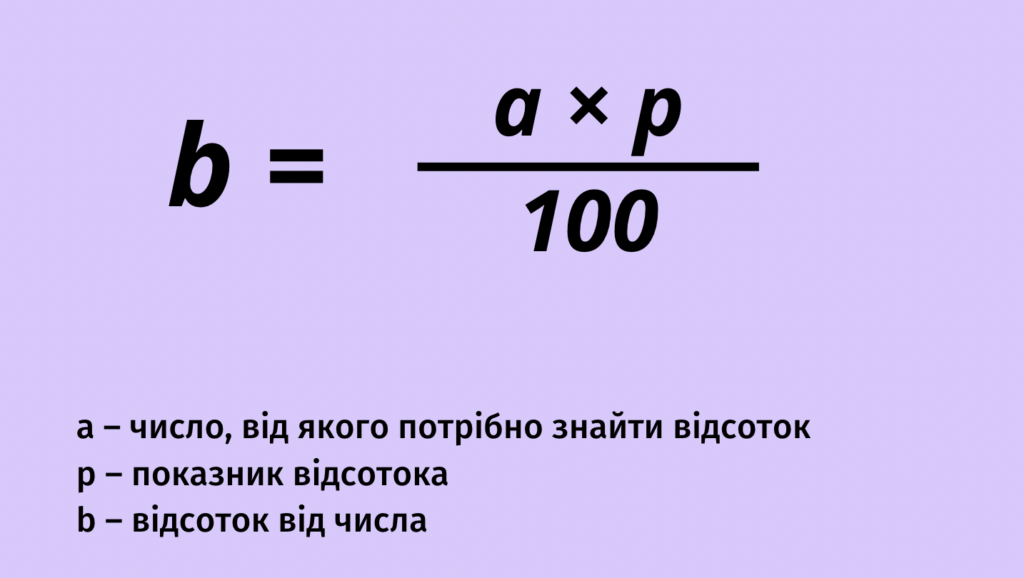
Подразумевается, что эта величина составляет некое количество процентов от общего количества разделов курса. Мама Тома собралась купить ему штаны, которые без скидки стоят рублей. Помогите найти маме Тома цену штанов с учётом скидки. Автомобиль едет по маршруту длиной в 45 км. Известно, что он проехал уже 18 км. Какой процент от всего пути проехал автомобиль? Ищем процент пройденного пути от всего пути. Подбираем репетитора под любые цели. Уроки ведут действующие эксперты ЕГЭ, кандидаты наук с опытом работы от 5 лет.
Составим индивидуальный план подготовки и гибкое расписание — можно учиться из любого места и совмещать со школой или работой. Методисты Тетрики следят за всеми занятиями, фиксируют прогресс учеников и оценивают качество онлайн-уроков. А репетиторы отправляют обратную связь родителям после каждого урока.
Главная Учебник Задачи на проценты. Автор: Команда Тетрики. Задачи на проценты Учебник Время чтения: 3 мин. Виды задач на проценты Задачи на проценты бывают следующих видов: Необходимо найти процент от числа или величины. Найти число или величину по заданному значению его процентов. Найти, сколько процентов одно число или величина составляет от другого.
Алгоритм решения задач на проценты Любой вид задачи можно решить при помощи одного алгоритма. Скорее запоминайте! А ещё можете сохранить эту памятку, чтобы всегда была под рукой! Читайте по теме: Длина окружности и площадь круга. Педсовет — сообщество для тех, кто учит и учится.

С нами растут профессионалы. Хотите успевать за миром и трендами, первыми узнавать о новых подходах, методиках, научиться применять их на практике или вообще пройти переквалификацию и освоить новую специальность?
Всё возможно в нашем Учебном Центре. На нашей платформе уже более 40 онлайн-курсов переквалификации и дополнительного образования. Слово процент от латинского слова pro centum, что буквально означает «за сотню» или «со ста».

Идея выражения частей целого постоянно в одних и тех же долях, вызванная практическими соображениями, родилась еще в древности у вавилонян. Ряд задач клинописных табличек посвящен исчислению процентов, однако вавилонские ростовщики считали не «со ста», а «с шестидесяти».
Проценты были особенно распространены в Древнем Риме. Римляне называли процентами деньги, которые платил должник заимодавцу за каждую сотню. От римлян проценты перешли к другим народам Европы. Долгое время под процентами понимались исключительно прибыль или убыток на каждые сто рублей. Они применялись только в торговых и денежных сделках. Затем область их применения расширилась, проценты встречаются в хозяйственных и финансовых расчетах, статистике, науке и технике.
Ныне процент — это частный вид десятичных дробей, сотая доля целого принимаемого за единицу. В школьном учебнике "Математика, 5«,авторов Н.
Виленкина и др. Там, в частности, говорится, что этот знак произошел в результате нелепой опечатки, совершенной наборщиком.
В г. Еще больше полезных материалов — в Телеграм-канале Педсовета. Подписывайтесь, чтобы не пропускать свежие статьи и новости. Современная жизнь делает задачи на проценты актуальными, так как сфера практического приложения процентных расчетов расширяется. Вопросы инфляции, повышение цен, рост стоимости акций, снижение покупательской способности касаются каждого человека в нашем обществе.
Планирование семейного бюджета, выгодного вложения денег в банки, невозможны без умения производить несложные процентные вычисления. Сами проценты не дают экономического развития, но их знание помогает в развитии практических способностей, а также умение решать экономические задачи. Обдуманное изучение процентов может способствовать развитию таких навыков как экономичность, расчетливость.
В вариантах вступительных экзаменов встречаются задачи на проценты, и эти задачи часто вызывают затруднения у школьников. Причина в том, что тема «Проценты» изучается в младших классах, причем непродолжительно, закрепляется в 7 классе при решении задач на повторение, а в старших классах к этой теме совсем не возвращаются.
Так, пересмотрев школьные учебники по математике, по которым обучаются ученики нашей гимназии, я выяснила, что в учебнике «Алгебра, 9», под ред. Теляковского, задач, в которых упоминается слово «процент», всего три. В учебнике «Алгебра и начала анализа, » под ред Колмогорова А. Н задач на проценты и процентную концентрацию черыре. Но, задачи на проценты уже встречались в вариантах единого государственного экзамена в , , годах.
Предлагается такая задача и в демонстрационном варианте года. Поэтому, изучение наиболее часто встречающихся типов задач на проценты, считаю актуальным. Объектом исследования является изучение различных типов задач по теме «Проценты». Изучая эту тему по сборникам для поступающих в вузы[5], я пришла к мнению, что многие задачи авторы сборников предлагают решать с использованием специальных формул, которых в школьных учебниках классов, когда и изучаются эти темы, нет.
Предмет исследования : решение задач на проценты и процентное содержание, концентрацию, смеси и сплавы с преимущественным использованием основных правил действия с десятичными и обыкновенными дробями.
Цель работы. Составить практическое пособие по решению задач на проценты для школьников. Практическая значимость работы. Данное пособие по решению задач на проценты будет интересно не только школьникам класса, которым интересна математика. Здесь найдут много полезного и выпускники школ, и абитуриенты при подготовке к выпускным и вступительным экзаменам.
В данной главе приводятся примеры задач, которые решаются с применением определения, что такое один процент, как выразить дробь в процентах и правилам нахождения части дроби от числа, и числа по значению его части дроби , то есть это те темы и задачи, которые рассматриваются в школе. Обращаем внимание, что существуют и другие способы решения простейших задач на проценты, например, составляют пропорции на каждом шаге, но в этом случае решение становится на несколько шагов длиннее. Мы же видим свою задачу в нахождении более быстрых способов решения таких задач, в связи с тем, что в настоящее время редкий тест по математике для абитуриентов, обходится без задач, в которых не упоминались бы проценты.
Сотая часть метра — это сантиметр, сотая часть рубля — копейка, сотая часть центнера — килограмм. Люди давно замети, что сотые доли величин удобны в тактической деятельности. Потому для них было придумано специальное название — процент. Значит одна копейка — один процент от одного рубля, а один сантиметр — один процент от одного метра. Один процент — это одна сотая доля числа. Деление на можно заменить умножением на 0, Токарь вытачивал за час 40 деталей. Применив резец из более прочной стали, он стал вытачивать на 10 деталей в час больше.
На сколько процентов повысилась производительность труда токаря? Решение : Чтобы решить эту задачу, надо узнать, сколько, процентов составляют 10 деталей от Для этого найдем сначала, какую часть составляет число 10 от числа Мы знаем, что нужно разделить 10 на Получится 0, При плановом задании 60 автомобилей в день завод выпустил 66 автомобилей.
На сколько процентов завод выполнил план? Решение : — такую часть составляют изготовленные автомобили от количества автомобилей по плану. На сколько процентов 10 больше 6? На сколько процентов 6 меньше 10? Решение : 1. Бронза является сплавом олова и меди. Сколько процентов сплава составляет медь в куске бронзы, состоящем из 6 кг олова и 34 кг меди? Ответ : Сколько надо взять хлопка-сырца, чтобы получить кг волокна.? Сколько получится сухих грибов из 22 кг свежих? Решение : 1 Ответ : 2,5 кг.
Сплав содержит 10 кг олова и 15 кг цинка. Каково процентное содержание олова и цинка в сплаве? Решение : Процентное содержание вещества в сплаве — это часть, которую составляет вес данного вещества от веса всего сплава. Это означает, что чистого серебра в сплаве г. Отношения объема чистой компоненты в растворе ко всему объему смеси называется объемной концентрацией этой компоненты.
Решение : Пусть к 20 кг первого сплава нужно добавить х кг второго сплава. В 20 кг первого сплава содержится 0,4. Составим уравнение:. Вклад, вложенный в сбербанк два года назад, достиг суммы, равной руб.
На сколько процентов мартовская цена изменилась по сравнению с январской? Если х — январская цена нефти, то февральская цена нефти равна. В данной главе рассматривается выборка задач из различных источников, которые охватывают весь теоретический материал, который излагался выше, предлагаем свои решения. Отметим, что предложенный способ решения не является единственным. Задача 1. Товар стоил тысячу рублей.
Сколько стал стоить товар? Пусть товар стоил руб. Задача 2. Собрали кг грибов. Какой стала масса этих грибов после подсушивания?
Задача 3. Цена входного билета на стадион была 1 рубль 80 копеек. Сколько стал стоить билет после снижения? Пусть зрителей, до понижения цены, на стадион приходило А чел. Задача 4. По дороге идут два туриста. Кто из туристов идет быстрее и почему?
Пусть второй турист делает а шагов, каждый из которых равен в, тогда ав это длина пройденного пути.